降维方法认为,不同维度之间的数据包含相关性,所以可以通过某种映射方法将数据从高维空间映射到低维空间。
显然,降维必然会带来信息丢失,所以数据降维方法希望将降维带来的信息丢失造成的影响降低。
判断数据是否适合降维(充分性检测)
如果数据不同维度之间的联系非常小,那么无论怎么设计降维方法都意义不大,降维等价于信息的白白丢失。所以通常我们需要先判断数据是否适合做直接的降维,如果数据本身就不适合降维,那么可能需要在降维之前优先考虑联合维度以构造数据间的相关性。
1、协方差
当谈论数据之间的相关性时,非常自然的能够想到通过协方差进行度量:
\[
\sigma(x,y)=\frac{1}{n-1}\sum_{a}^{b}(x_i-\bar{x})(y_i-\bar{y})
\] 构造协方差矩阵: \[
\Sigma=\begin{bmatrix}\sigma(x_1,x_1)&\cdots&\sigma(x_1,x_d)\\\vdots&\ddots&\vdots\\\sigma(x_d,x_1)&\cdots&\sigma(x_d,x_d)\end{bmatrix}\in
R^{d\times d}
\]
协方差为正意味着两个维度为正相关,反之则为负相关。值越大则越相关。
大部分的相关系数都是基于协方差构造,本质大同小异。
2、KMO检验
主成分分析之前,通常通过KMO检验判断原始数据是否适合进行主成分分析。
KMO检验值越大证明越适合进行主成分分析 ,通常认为值在0.6以下时不适合进行主成分分析。
python代码如下:
1 2 3 4 5 6 7 8 9 ''' 检查变量间的相关性和偏相关性,取值在0-1之间; KMO统计量越接近1,变量间的相关性越强,偏相关性越弱,因子分析的效果越好 ''' from factor_analyzer.factor_analyzer import calculate_kmokmo = calculate_kmo(df) print (f'KMO检验结果为:{kmo[1 ]} ' )
3、Bartlett球形度检验
Bartlett球形度检验是一种用于检验原始数据的各个变量之间是否具有较强的线性相关性的方法,是主成分分析的效度检验指标之一。
Bartlett球形度检验的原假设是各个变量之间不存在线性相关性,即相关系数矩阵是一个单位阵。如果检验结果的p值小于 显著性水平(通常为0.05),则拒绝原假设,认为各个变量之间存在线性相关性 ,数据适合 进行主成分分析。相反,如果检验结果的p值大于显著性水平,则接受原假设,认为各个变量之间不存在线性相关性,数据不适合进行主成分分析。
python代码如下:
1 2 3 4 5 from factor_analyzer.factor_analyzer import calculate_bartlett_sphericitychi_square_value, p_value = calculate_bartlett_sphericity(df) print (f'卡方={chi_square_value} ,P值={p_value} ' )
降维方法
降维方法总览
降维方法综述 - 知乎
(zhihu.com)
线性降维方法
1、LDA(Linear discriminant
analysis)
如何理解线性判别分析(LDA)算法?能够简洁明了地说明一下LDA算法的中心思想吗?
- 知乎 (zhihu.com)
LDA算法的思想是将数据投影到低维空间之后,使得同一类数据尽可能的紧凑,不同类的数据尽可能分散。
两个假设:
原始数据根据样本均值分类 不同类的样本有相同的协方差矩阵
当然,在实际情况中,不可能满足以上两个假设。但是当数据主要是由均值来区分的时候,LDA一般都可以取得很好的效果。
如果假设不同的维度可以描述的性质可以被分为几类,使用LDA似乎也能自圆其说。
但是我们不知道他应该怎么分类,所以抛弃
2、PCA
主成分分析对不同维度之间的线性相关性要求较高,尝试过后效果不佳。
3、FA(Factor Analysis)
因子分析(Factor
Analysis)的原理与使用 - 知乎 (zhihu.com)
对于p维观测变量,FA假设每一个维度的变量可以表示为m个共因子和p个特殊因子的线性组合,其中m<p,从而实现了降维。
\[
\begin{aligned}&X_1-\mu_1=l_{11}F_1+l_{12}F_2+\ldots+l_{1m}F_m+\epsilon_1\\\\&X_2-\mu_2=l_{21}F_1+l_{22}F_2+\ldots+l_{2m}F_m+\epsilon_2\\\\&\ldots\\\\&X_p-\mu_p=l_{p1}F_1+l_{p2}F_2+\ldots+l_{pm}F_m+\epsilon_p\end{aligned}
\] 有矩阵形式 \[
X=\mu+L*F+\epsilon
\]
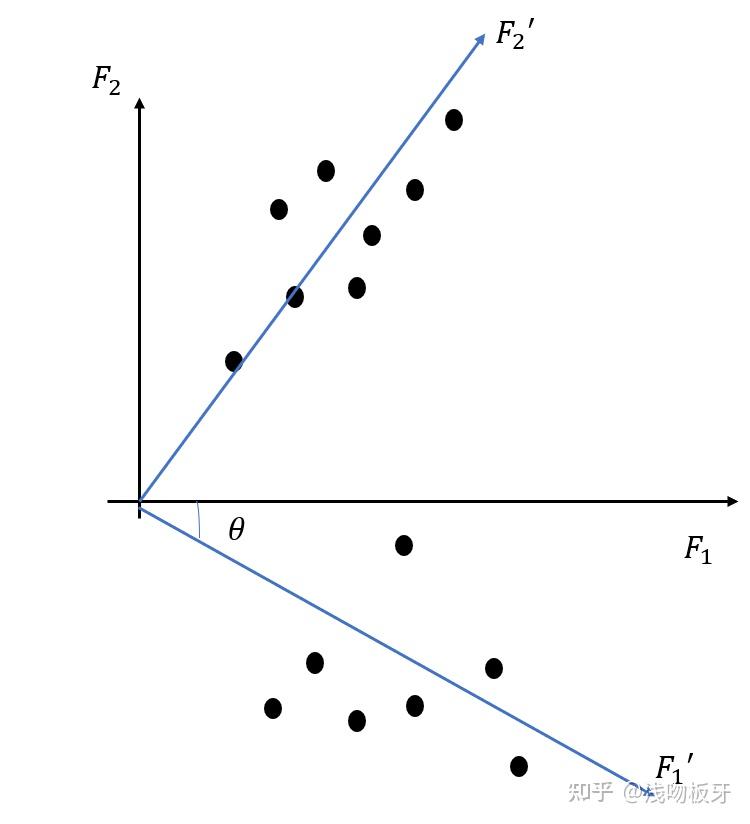
因子旋转
直接构造的主因子可能不具有很好的“解释性”或者“不好用”,所以我们期望通过不改变因子间相对关系的前提下进行旋转,使得主因子的解释性更强。
FA_因子旋转_正交
对于多维的主因子,我们通常保持因子之间的正交关系进行旋转,具体做法是使用Varimax方法 。
实验过程中,FA方法在面对高维数据时效率相当低,怀疑低效原因来自与因子旋转的过程。
非线性降维方法
1、LLE(Local Linear Embedding)
LLE旨在处理流形(manifold)建模上的降维问题。
几何学中最伟大的发明之一——流形,其背后的几何直觉与数学方法
- 知乎 (zhihu.com)
流形是一个可以在局部范围内近似为欧几里得空间的空间
地球是圆的,但是地是平的。
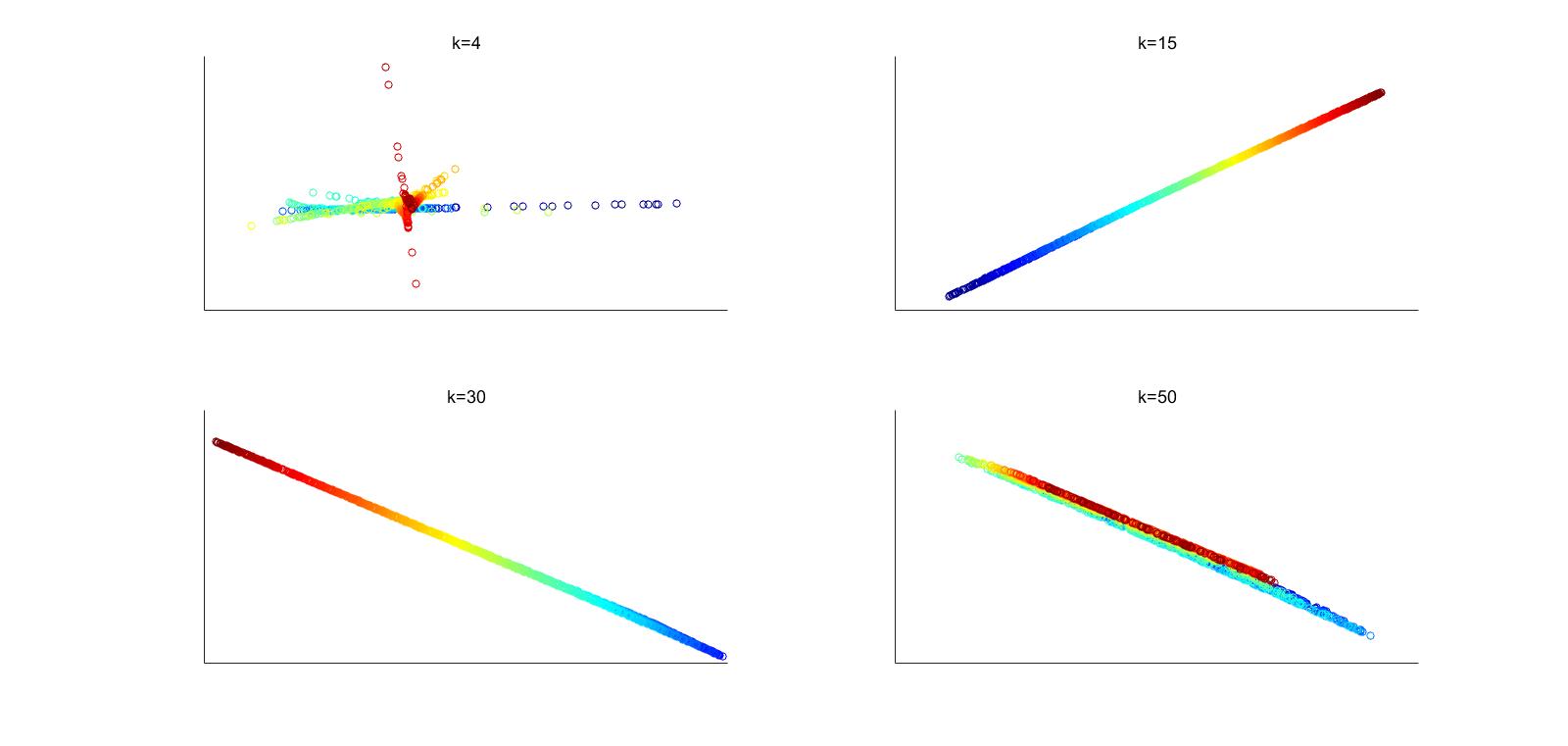
思想 :根据流形的性质,一个点可以被周围的k个点线性表示,所以用
KNN等方法找到临近的k个点,获得一组权重,然后期望这个权重在维度更低的k个向量上也可以组合为该点的低维表示。
简单来说,LLE降维最大的特点是维护了流形局部线性的性质
算法过程:
step1:
通过KNN求得每个数据的k近邻点 \[
N_i=KNN(x_i,k),N_i=[x_{1i},\ldots,x_{ki}]
\] step2:
求解权重系数矩阵W,即求解 \[
\arg\min_W\sum_{i=1}^N\|x_i-\sum_{j=1}^kw_{ji}x_{ji}\|^2,\\
s.t.\sum_{j=1}^kw_{ji}=1
\] 输入: \[
X=[x_{1},x_{2},\ldots,x_{N}],D\times N
\] 权重: \[
w=[w_1,w_2,\ldots,w_N],k\times N
\] step3:
映射到低维空间 \[
\begin{aligned}\arg\min_Y\Psi(Y)&=\sum_{i=1}^N\|y_i-\sum_{j=1}^kw_{ji}y_{ji}\|^2,\\&s.t.\sum_{i=1}^Ny_i=0,\\
&\sum_{i=1}^Ny_iy_i^T=NI_{d\times d}\end{aligned}
\]
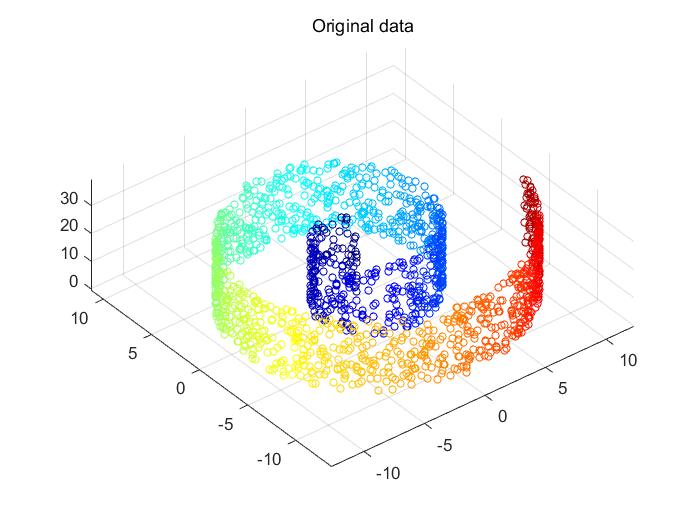
示意图
原图:
LLE_swiss_roll_new_data
2、LE(Laplacian Eigenmaps)
https://www2.imm.dtu.dk/projects/manifold/Papers/Laplacian.pdf
Laplacian EigenMaps
- 知乎 (zhihu.com)
LE从图的角度构建数据间的关系。图中的每个顶点代表一个数据,每一条边权代表数据之间的相似程度,越相似则权值越大。
LE假设每一点只与k个相邻点相似,与其他点的相似度为0。
简单来说,LE维护了降维之后点间的相似性。
算法流程
step1:
构造图;
通过KNN求k个邻近点。
step2:
赋权
Heat kernel: \[
W_{ij}=e^{-\frac{\|\mathbf{x}_i-\mathbf{x}_j\|^2}t}
\] 或Simple-minded: \[
W_{ij}=1
\] step3:
Eigenmaps,即可等效为优化问题 \[
\arg\min_{y}y^{T}Ly,\\
s.t.\ y^TDy=1
\] 其中L为Laplacian Matrix,L=D-W
 降维后:
降维后: